|
Home |
Das Rätsel der drei Türen von Jochen Paulus |
||||||||
|
Am so genannten Ziegenproblem bissen sich sogar Nobelpreisträger die Zähne aus. Deutsche Forscher haben endlich einen Weg gefunden, die Lösung anschaulich zu erklären Kaum eine andere mathematische Denkaufgabe hat die Gemüter
(auch die der ZEIT-Leser)
in den vergangenen Jahren so erhitzt wie das so genannte Ziegenproblem. Denn
dem normalen, angeblich »gesunden«, Menschenverstand läuft die mathematisch
korrekte Lösung derart zuwider, dass sich nur die wenigsten Zeitgenossen von
ihr überzeugen lassen. Nun aber scheint erstmals eine Methode gefunden, die Sprache
der Wahrscheinlichkeitsstatistik so zu übersetzen, dass sie selbst
Schulkindern verständlich wird und allen Zweiflern einleuchtend erscheint.
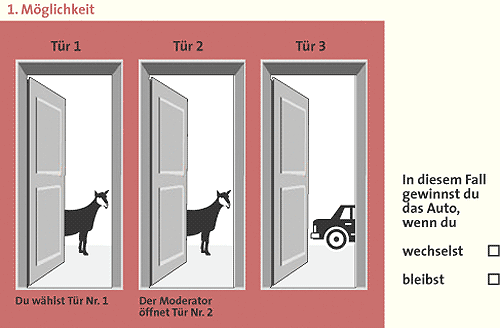
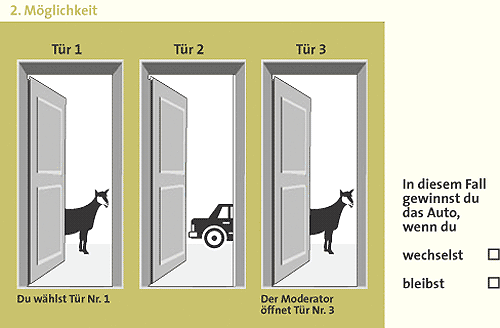
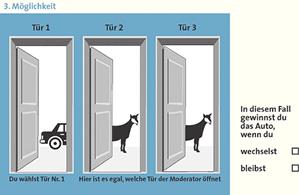
Die Ausgangssituation des Ziegenproblems lautet folgendermaßen: Sie sind Kandidat einer Fernsehshow und dürfen eine von drei verschlossenen Türen auswählen. Hinter einer der Türen wartet der Hauptgewinn, ein prachtvolles Auto, hinter den anderen beiden steht jeweils eine meckernde Ziege. Frohgemut zeigen Sie auf eine der Türen, sagen wir Nummer eins. Doch der
Showmaster, der weiß, hinter welcher Tür sich das Auto befindet, lässt sie
nicht sofort öffnen, sondern sagt geheimnisvoll: »Ich zeige Ihnen mal was!«
Er lässt eine andere Tür öffnen, sagen wir Nummer drei – und hinter dieser
steht eine Ziege und glotzt erstaunt ins Publikum. Nun fragt der Showmaster
lauernd: »Bleiben Sie bei Tür Nummer eins, oder wählen Sie doch lieber Nummer
zwei?« Was sollten Sie tun?
Dies ist das Ziegenproblem, das im angelsächsischen Sprachraum »Monty Hall Problem« genannt wird. Es geht auf die Spielshow Let's Make a Deal zurück, eine Art amerikanische Variante von Wetten, dass..., die von Monty Hall moderiert wurde und vor allem in den sechziger und siebziger Jahren populär war. Die amerikanische Autorin Marilyn vos Savant, die als Frau mit dem höchsten je gemessenen IQ gilt, stellte das Ziegenproblem im Jahre 1990 in ihrer regelmäßigen Magazin-Kolumne vor und löste damit eine weltweite Debatte aus, die bis heute anhält. Etwa 99 Prozent der mit dieser Aufgabe Konfrontierten sind der Meinung,
dass das Auto ebenso gut hinter der einen wie der anderen Tür stehen kann,
und fast 90 Prozent entscheiden sich angesichts dieser vermeintlichen
Sachlage dafür, bei der ursprünglichen Tür zu bleiben. Die statistisch
Vorgebildeten dieser Mehrheitsfraktion argumentieren ungefähr so: »Nachdem
der Moderator eine Ziege gezeigt hat, bleibt Ihnen eine Wahrscheinlichkeit
von eins zu zwei, die richtige Wahl zu treffen. Egal, ob Sie Ihre
Entscheidung revidieren oder nicht, die Aussichten bleiben die gleichen.«
Dies schrieb zum Beispiel ein promovierter Leser an Marilyn vos Savant.
Doch das Ziegenproblem gilt nicht umsonst als »Königin der Denk-Illusionen«. Die richtige Antwort lautet: Es ist besser, die Tür zu wechseln. Doch Marilyn vos Savant gelang es nicht, ihre Leser davon zu überzeugen. Das bewies der zumeist wütende Tenor von rund zehntausend Zuschriften (»Die Niete sind Sie!«). Selbst zwei Drittel der Briefschreiber aus Universitäten waren gegen sie. Ähnlich stark war die Resonanz auf zwei Artikel in der ZEIT vor über zehn Jahren. Am Ende entschloss sich deren Autor gar, dem Thema ein eigenes Buch zu widmen (Gero von Randow: Das Ziegenproblem, Rowohlt Verlag). Selbst Paul Erdös, genialer Mathematiker des 20. Jahrhunderts und noch dazu Statistiker, beharrte lange auf der falschen Lösung. Seine Kollegen konnten ihn erst mit Hilfe einer Computersimulation überzeugen. Dabei wurden einfach 100 Runden durchgespielt. Wechseln erwies sich als besser. Eigentlich ist die Lösung ganz einfach. Eigentlich An der richtigen Lösung kann es mithin keinen Zweifel geben. Dennoch bleibt die Frage: Wie erkläre ich es einem Mathematiker oder gar einem mathematikfernen Normalbürger? Seit der großen Kontroverse probierten Didaktiker und Psychologen diverse Erklärungswege aus. Doch beim Großteil ihrer Versuchspersonen ernteten sie stets nur Verständnislosigkeit. Erst in diesem Jahr waren Stefan Krauss vom Berliner Max-Planck-Institut für Bildungsforschung und seine Mitarbeiter erfolgreich. Sie konnten das Problem, an dem selbst Nobelpreisträger gescheitert sein sollen, so erklären, dass sogar Schüler die richtige Lösung verstanden. »Der entscheidende Trick dabei war sicherlich, dass wir nicht die Aufgabe analysiert haben, denn das wurde zehn Jahre lang gemacht«, sagt der Psychologe Krauss. »Wir haben einfach mal geschaut: Die wenigen, wenigen Leute, die das richtig machen – einige gibt es nämlich immer –, was machen die eigentlich? Was denken die?« Die Befunde kombinierten die Forscher mit Erkenntnissen der Denkpsychologie zu ihrer funktionierenden Erklärung. Als Schlüssel erwies es sich, auch die Perspektive des Showmasters einzunehmen statt nur die des Kandidaten. Der zweite Kunstgriff besteht darin, nicht über abstrakte Wahrscheinlichkeiten zu räsonieren, sondern konkrete Fälle durchzuspielen. Es gibt ja nur drei Türen, und hinter einer muss das Auto stehen. Die drei – gleich wahrscheinlichen – Möglichkeiten lauten: Erstens: Das Auto steht hinter Tür eins. In unserem Beispiel hat der Kandidat diese Tür gewählt, es wäre also sinnvoll, bei dieser Tür zu bleiben, was immer der Showmaster tut. Zweitens: Das Auto steht hinter Tür drei. Dann muss der Showmaster natürlich Tür zwei öffnen. Denn er darf nicht das Auto hinter Tür drei zeigen, und er darf auch nicht enthüllen, ob der Kandidat mit Tür eins richtig liegt. In diesem Fall ist also das Wechseln zur verbleibenden Tür drei vorteilhaft. Drittens: Das Auto steht hinter Tür zwei. Der Fall ist ein Spiegelbild des vorigen, nur dass der Showmaster diesmal Tür drei öffnet. Wieder verhilft Wechseln zur verbleibenden Tür zum Gewinn. Fazit: Wer wechselt, gewinnt in zwei von drei Fällen, also empfiehlt sich Wechseln. So einfach ist das. Fast schon zu einfach, wie das Krauss-Team bei einem Test in einem Berliner Gymnasium feststellen musste. Die Schüler dort erhielten keine komplette Lösung, wurden aber mit mehreren Grafiken auf den richtigen Weg geführt: Das wichtigste Schaubild (siehe Abbildung) zeigte die drei Möglichkeiten und die jeweilige Reaktion des Moderators. Die richtigen Schlussfolgerungen mussten die Schüler selbst ziehen. Bei den Fünft- und Siebtklässlern schaffte dies immerhin knapp die Hälfte, in der neunten und elften Klasse waren es sogar über 80 Prozent. Doch ausgerechnet im Leistungskurs Mathematik der 13. Klasse brach die Leistung dramatisch ein, wie die konsternierten Forscher bei der Auswertung feststellten. Der Mathe-Leistungskurs glaubte an eine Falle Das Team machte sich also noch einmal zu den Mathe-Cracks auf, um bei einem lockeren Gespräch herauszufinden, was da passiert war. Wie sich herausstellte, hatten die Leistungskursler die Aufgabe spielend verstanden. Aber sie konnten nicht glauben, dass Bildungsforscher einen Mathematik-Leistungskurs mit einem derart simplen Problem behelligen würden. Also vermuteten sie eine Falle und gaben wider bessere Einsicht die verkehrte Antwort. Und was nützt der Triumph der Didaktik? Schließlich muss kaum jemand sich jemals mit hinter Türen versteckten Ziegen und Autos herumschlagen. Für Krauss lautet die Lehre, dass man nicht vorschnell behaupten sollte, Schüler könnten schwierige Aufgaben einfach noch nicht verstehen. Wenn das berüchtigte Ziegenproblem vermittelbar ist, dann sei es mit genügend Forschungsaufwand »eventuell möglich, ihnen jedes andere Problem genauso näher zu bringen«.
|